算一下STEEM当年的实际年通胀率

在之前的文章《STEEM是如何产出以及如何分配的》中，我们知道了新产生的区块生成STEEM的计算公式。

(图源：pixabay)

公式如下：

auto new_steem = ( props.virtual_supply.amount * current_inflation_rate ) / ( int64_t( STEEM_100_PERCENT ) * int64_t( STEEM_BLOCKS_PER_YEAR ) );

也就是说，用当前供应量x当前通胀率计算出年新产生的STEEM总量，再除以每年产生的区块数来计算当前每块新增STEEM

乍一听貌似没啥问题，但是其中涉及有两点，一个是复利问题，另一个是通胀率缩窄。

复利问题

先说复利问题，如果单独靠文字描述可能有些抽象，我们举个例子，假如我们有10000元，存银行，年利率10%，这个大家轻易可以算出来，到期新增了1000元，貌似没什么疑问。

但是STEEM的做法是，我每3秒给你发一次利息，利息还可以计算到本金里，继续享受10%的利息，这就是所谓的复利，用在高利贷上，叫做利滚利。

为了便于展示，我们不模拟3秒发一次利息，也不每天发一次利息，就按每月发一次，来看看复利的威力吧。假设我们有10000元本金，年利率10%，按STEEM的机制按月分红，那么12个月的情况大致如下：

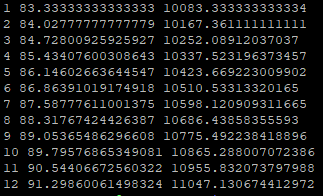
我们多得47元，相当于多拿了0.47%的利息。

这还是因为我们年利率低，如果年利率为100%，那么结果就更夸张了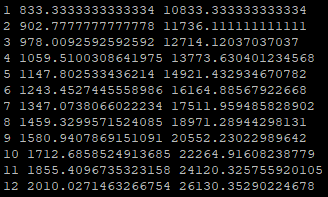

多得6130元，相当于多拿了61%了的利息哦。

我们知道每250K区块，通胀率是缩减的。继续举例子，相当于上个例子，每个月利息下降1%，那么继续假设我们有10000元本金，年利率10%，按STEEM的机制按月分红，年利率每月下降0.5%，那么12个月的情况大致如下：

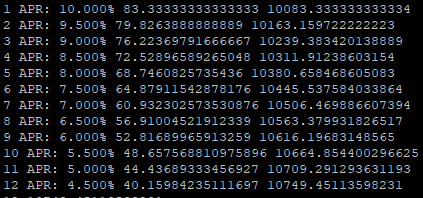
诺，就是这样，尽管按复利算，我们赚了，但是因为利率缩减，我们这次亏大发了😭

按照年化的定义，我理解无论从STEEM的哪个块算起，当前块对应的年化利率乘以当前块的总供应量，再加上当前总供应量，就是一年后的供应量。

就好比10000元，年化利率10%，一年后我拿到11000 元，这不应该有啥分歧。

然而上边两个因素会导致一些变化：

具体一年下来我们是多得还是少得呢？这个和通胀率的高低以及缩窄的快慢有关。简单来讲，通胀率越高我们多得的越多，缩窄速度越快我们多得的越少。

为了看看现在到底是多得还是少得，我按STEEM的规则模拟生成一年的区块，然后算一下实际年通胀率。

结果如下：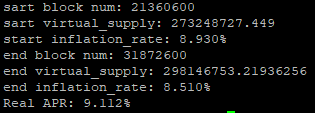

也就是说，当前实际上一年的通胀率为9.112%，高于我们开始时计算出来的8.930%。

具体偏高还是偏低取决于当前通胀率以及通胀率缩窄的速度。

你问算这个有什么用呢？实际上一点用都没有，我就是闲着无聊验证一下。如果有年度最无聊奖，当颁发给我：）

# apr, cn, cn-programming, steem, steemdev