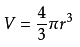昨天在微信群里浅水,看他们聊天,突然说到了IPv6地址,一个朋友说到IPv6取之不尽用之不竭,另一个朋友说了一句话:IPv6可以给每个原子编个号。
(图源 :pixabay)
好吧,因为宇宙是非常大的,甚至凭我的大脑都很难想象宇宙有多大,诺大的宇宙当中有多少星球有多少原子更不必说了,所以我认为朋友的意思应该是IPv6可以给地球上的每个原子编个号。
那么IPv6真的可以给地球上的每个原子编个号嘛?我觉得有点夸张,于是就想验证一下。
IPv6地址数量
首先,有多少个IPv6地址呢?
我们知道IPv6的地址长度有128位,所以理论上会有2128,这么多个地址。
如果用Python语言来计算的话,那么IPv6为:
ipv6=2**128
等于这么多个(请原谅我根本数不过来)😳:
340282366920938463463374607431768211456
地球上有多少个原子
知道了IPv6地址的数量,我们再来估算一下地球上有多少个原子。要想知道这个,我想到的办法是计算一下地球的体积,再除以原子的体积。
地球体积
那么地球的体积是多少呢?由于太阳引力的问题,地球不是个正规的圆球,百度百科相关描述如下:
地球赤道半径6378.137千米,极半径6356.752千米,平均半径约6371千米。
反正是估算,那么我们就按它是个规则的圆球好了,使用平均半径6371千米作为圆球半径。
圆球体积的计算公式我们小学都学习过:
用Python计算,地球体积:
from math import pi as PIr = 6371 * 1000earth_v = 4/3*PI*(r**3)
也就是说,地球体积大致为这么多立方米(M2):
1.0832069168457536e+21
注:大气层中也有原子,上述体积没有计算大气层,不过反正是估算嘛。
原子体积
地球体积足够大了,但是原子的体积可是足够小的啊。学习初中化学的时候,我们就知道了,不同原子的大小是不一样的啦。
从百度上找了半天资料,普遍的说法是一般来讲,原子的半径约为10-10m,当然了,这个值肯定不是精确的,但是反正我们是估算,数量级差不多就行啦。
用Python计算,原子体积:
r_atom = 10**(-10)atom_v = 4/3*PI*(r_atom**3)
计算出来原子的体积约为这么多立方米(M2):
4.188790204786391e-30
原子数量
所以,地球上的原子个数估算为:
atom_c = earth_v / atom_v
也就是说初略估算,地球上原子数量约为(个):
2.5859660281099996e+50
IPv6 vs 地球上原子数量
这时候我们再来看看IPv6是否可以分配到地球上的每一个原子:
ratio = ipv6 / atom_c
计算出来的结果为:
1.3158810410577592e-12
也就是说,IPv6 地址远远不够分配到地球上的每一个原子上。
结论
IPv6 地址远远不够分配到地球上的每一个原子上。
不过关于IPv6地址还有一个说法:
IPv6地址数量号称可以为全世界的每一粒沙子编上一个地址。
(引用来源:

(图源 :pixabay)
假设地球都是由沙子组成,假设沙子的半径是均匀的0.01mm,那么大致估算下来,那么每粒沙子大致可以分配到1315个地址,看来,真的可以给每一粒沙子编上一个地址。
(本文仅供无聊消遣,不保证方法和计算一定无误,欢迎专家批评指正)
相关链接
https://steemit.com/~witnesses type in
oflyhigh and click VOTE
Vote @oflyhigh via Steemconnect
Thank you!
This page is synchronized from the post: ‘有多无聊:IPv6地址和原子’