在之前的文章中，我们学习并测试了Memo加密的原理，一个关键性结论就是：

Pub(Alice) * Priv(Bob) = Pub(Bob) * Priv(Alice)

(图源 ：pixabay)

而这个乘积就是被当作Memo加密的密钥来用的，一般代码中称其为：shared_secret。

错误的探索

不过看steem-python代码中，只用了这个乘积的x部分。这让我突发奇想，既然只用到乘积中的x部分，那我是否可以只用x部分参与计算呢？

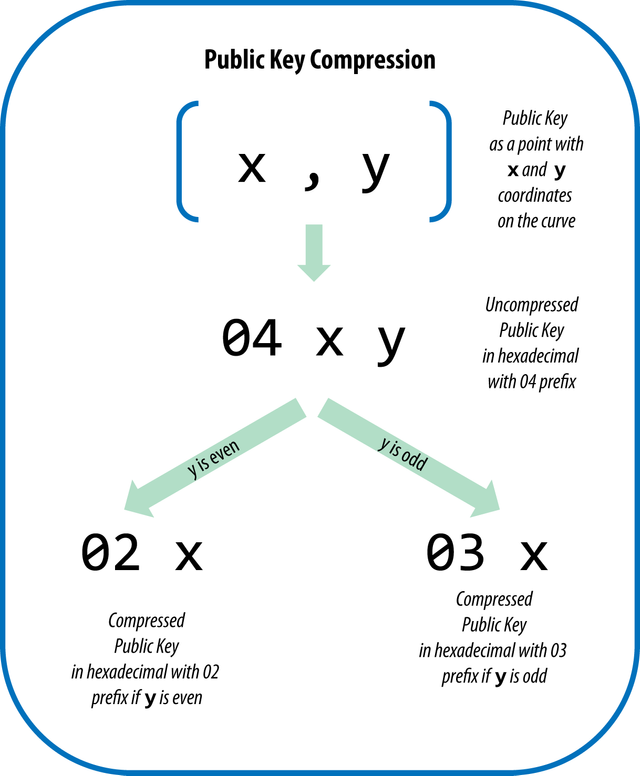
要知道我们使用的公钥都是压缩过的公钥（亦即只取公钥中的x部）:

而运算时，一般都是要先恢复成压缩前的公钥(通过x部算出y部，这极大增加了运算量，如果可以直接用，岂不美哉？

然而事实给了我无情的打击，以下测试代码说明了一且：

pa = ecdsa.SigningKey.from_string(sa, curve=ecdsa.SECP256k1).verifying_key.pubkey.point
print((pa*100).x() == pa.x()*100)

以上代码输出为：False

解读一下，就是用椭圆曲线上的点100再取x部，和椭圆曲线上的点取x部再乘以100并不相同*。

继续探索

想想也是，如果椭圆曲线的乘法就是把x, y乘以对应的数值，那还是椭圆曲线吗？虽然之前探索的方向错误了，但是也增长了见识，不算太亏。

有朋友问我，Pub(Alice) * Priv(Bob) = Pub(Bob) * Priv(Alice)这个结论应该没错，但是有推导吗?

这下难住了我，不过我想想之前学习公钥时学到的内容，貌似得出上述结论并不是很难。

还是要回到椭圆曲线上来：

我们知道，私钥(k)到公钥(K)计算公式：

K=k∗G

其中小k是我们的私钥，G是生成点，K是结果亦即公钥是曲线上的另外一个点。那么假设两组公私钥(K1, k1)以及(K2, k2)分别是Alice以及Bob的公私钥对，那么我们就有如下关系：

K1=k1∗G
K2=k2∗G

那么Alice的私钥乘以Bob的公钥就是：

`=k1K2`*
`=k1(k2∗G)`*
`=k2(k1∗G)`*
`=k2K1`*

所以Pub(Alice) * Priv(Bob) = Pub(Bob) * Priv(Alice)是可以证明的。

公钥的点

我们的公钥都是STMxxx的形式，要怎么还原成椭圆曲线上的点呢？

答案是可以用如下代码实现：

memo_key = 'STM5jy6R2yw6ZdQoUZZxcVCZ2R7TNpbrXzt4BGpAgnRXYrzwjsVvY'
memo_raw= gphBase58CheckDecode(memo_key[3:])
V = ecdsa.VerifyingKey.from_string(unhexlify(memo_raw), curve=ecdsa.SECP256k1)
P = V.pubkey.point

压缩公钥还原的过程是在ecdsa.VerifyingKey.from_string中完成的，其实我们可以直接调用静态方法ecdsa.VerifyingKey._from_compressed那样会直接返回一个点，而不是一个VerifyingKey类实例了。

总之，无论如何我还是老老实实地让他们去做乘法吧，不再妄想把x部先拆出来再做计算了，太囧了。

相关链接

• 每天进步一点点：探索memo加密的理论基础

This page is synchronized from the post: ‘每天进步一点点：继续探索memo加密 & 椭圆曲线’