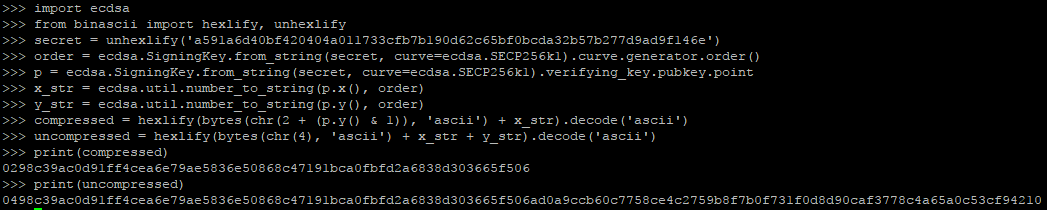
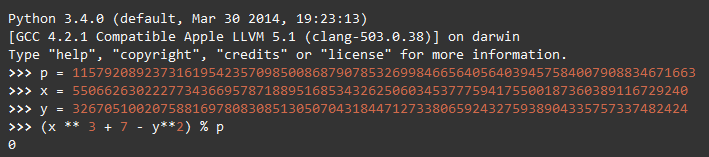
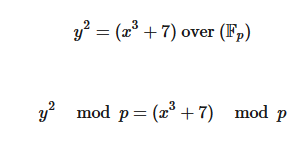之前写了一系列比特币私钥、公钥、地址有关的帖子

• 学习了一下Base58编解码
• 继续学习Base58以及Base58Check
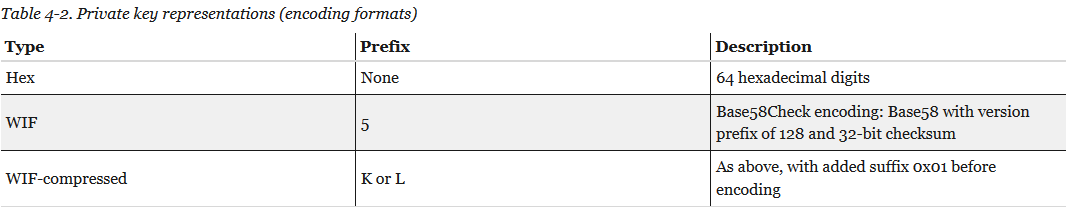
• 继续学习比特币的私钥 & 私钥的表示方法
• 每天进步一点点： 学习比特币的公钥
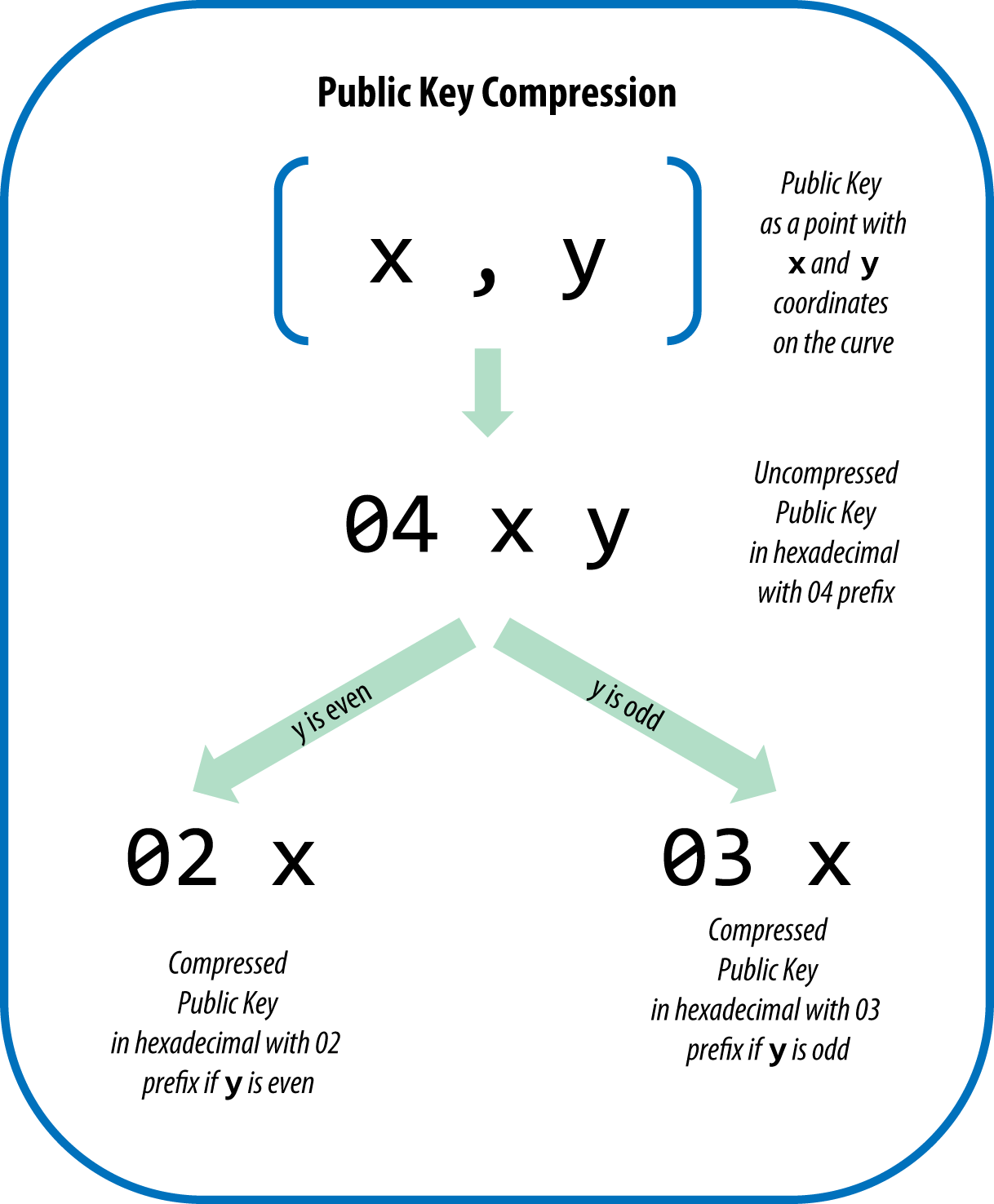
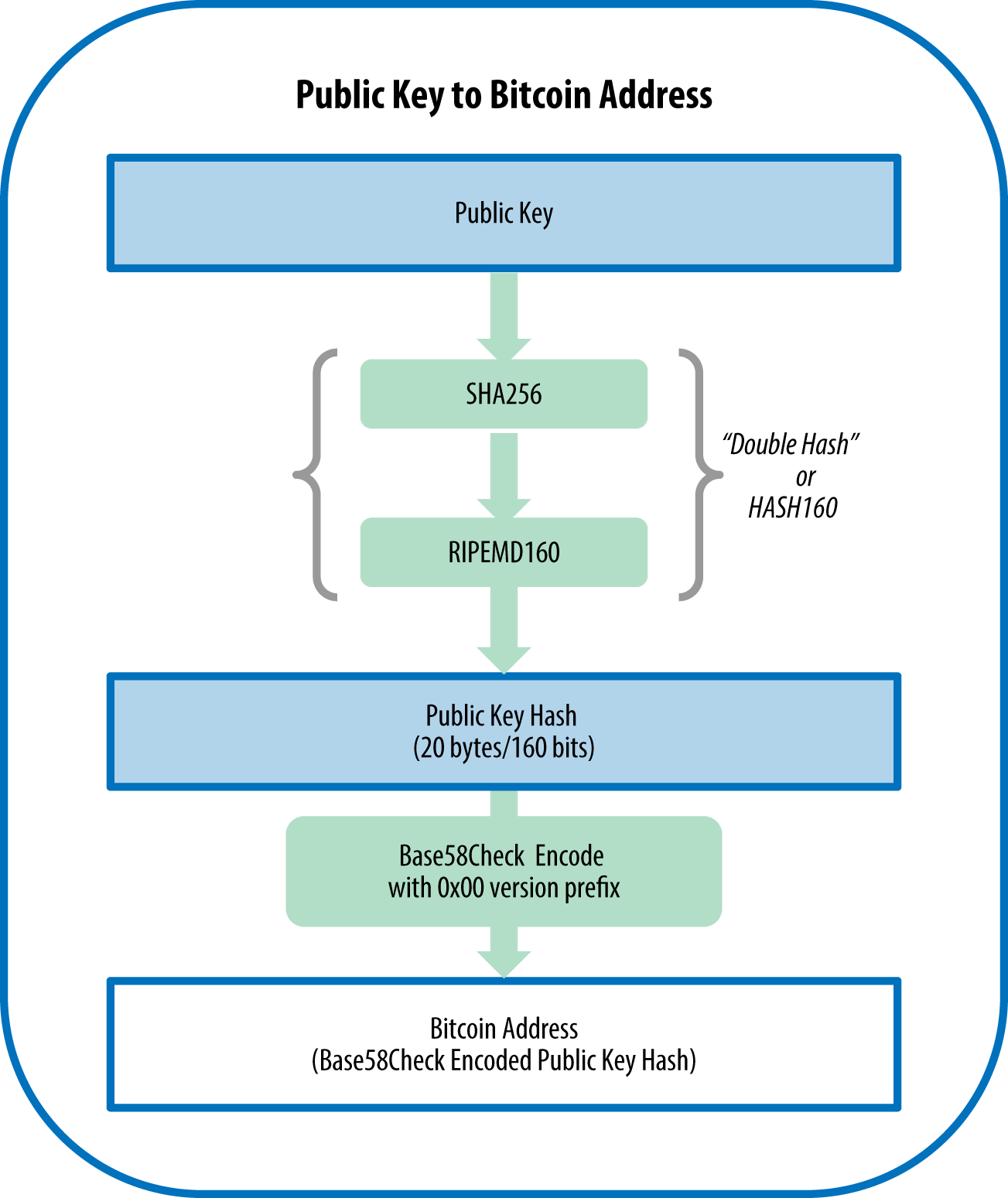
• 每天进步一点点： 比特币的公钥压缩与地址
• 真金白银出真知： 测试一下生成的比特币地址😭😭

有朋友私下里对我表示很关心： 是不是闲的?
其实我做这些都是为了迎接比特币的分叉。

分叉很迷糊

话说原本都说好了，8月1号不分叉，然后一夜之间画风又变了，说8月1日肯定分叉。
然后又说这个交易所支持，那个交易所不支持的，彻底迷糊。
搞得我们这些菜鸟晕头转向。

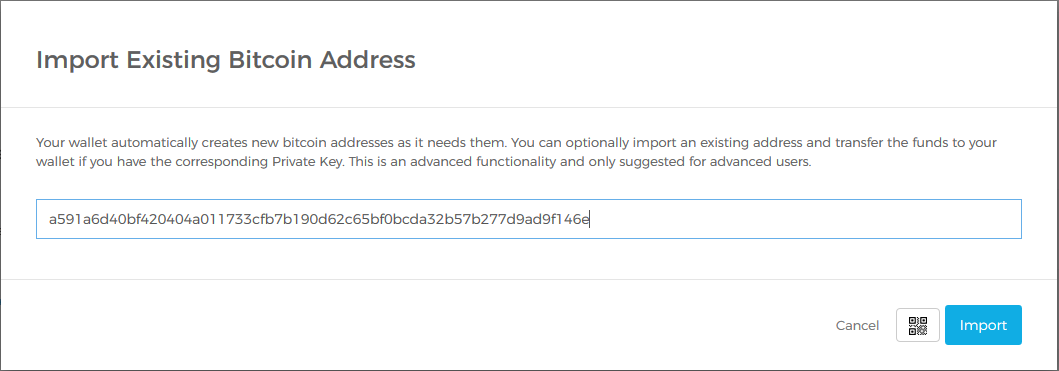
blockchain.info 私钥

不能直接取私钥

我咨询了一下专家，说币放在blockchain很安全，因为blockchain.info可以拿到私钥。
包括 @deanliu 老师也这么和我说
然后我去找了半天，也没找到取得私钥的地方
后来网上搜索了一下，说新版本的blockchain.info不能直接导出私钥了

间接方式也很麻烦

既然不能直接，那么就意味着可以用间接曲折的方式实现喽
百度了一下，果不其然，然而那个曲折劲啊
还要依赖第三方的脚本，总之我是很迷糊

创建新的私钥&地址

然后用看到中文区的朋友 @kenchung 的这篇文章

• How to get the private key of your Bitcoin address on Blockchain.info? 如何在Blockchain.info上獲取你比特幣地址的私鑰?

仔细拜读了一下，原来不是直接从Blockchain.info上获得私钥
而是用https://www.bitaddress.org 生成一组新的私钥地址对
然后把这个导入到Blockchain.info钱包
再把币都转过来，也不失为一种好方法

自己生成私钥&地址

话说我觉得 @kenchung 的方法不错
然后我又咨询持币数万的大佬们
大佬们有的说那个生成地址的工具安全，有的说不安全，有的建议我review全部代码（干脆杀了我吧），有的建议我下core钱包，据说130G，而且据说等我同步完，可能就10月份了。

总之，我又迷糊了😵😵😵😵😵。

然后又有大佬说，他们都是自己写钱包
我想了想，写钱包一点也不懂，生成给地址和私钥还应该有一定的可行性吧
估计有机会在8月1日之前完成。

于是就有了这一系列的学习过程诞生。

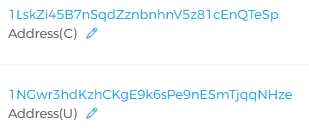
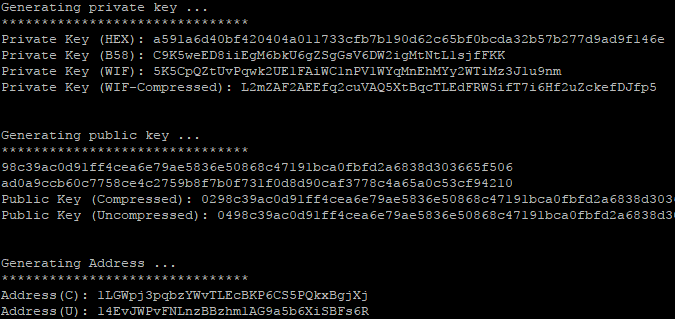
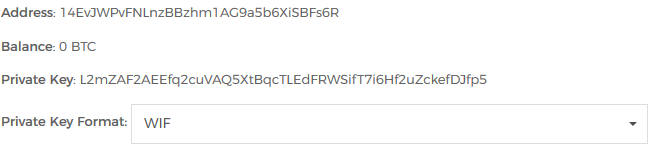
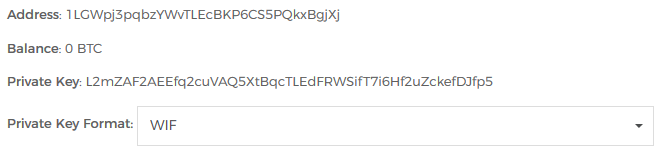
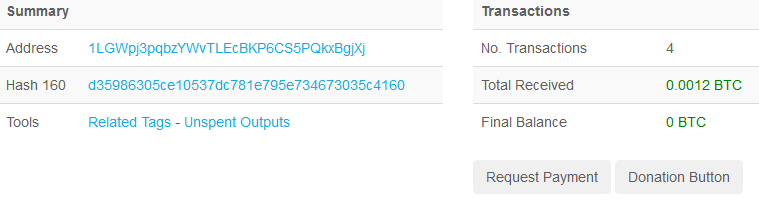
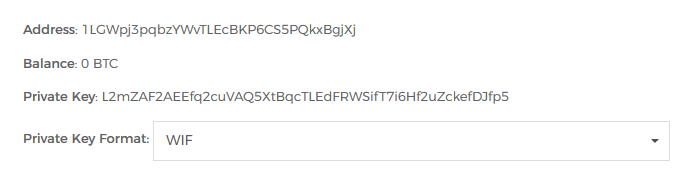
最终也生成了一组私钥和地址。
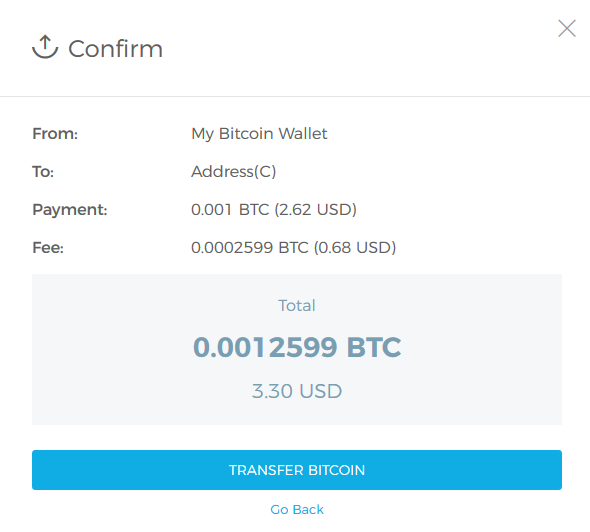
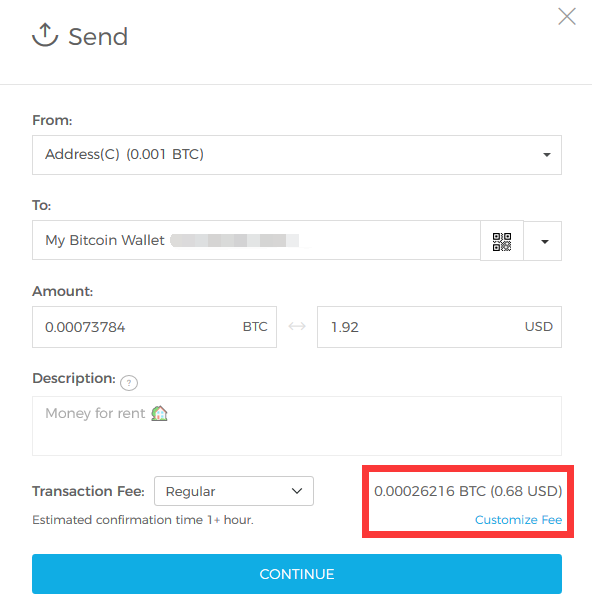
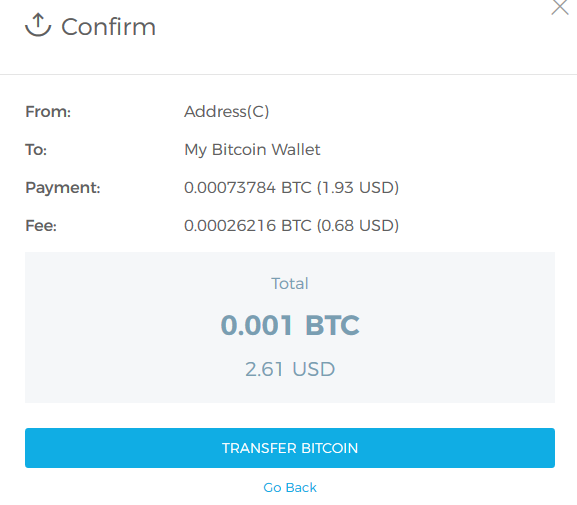
然后昨晚把比特币都扔自己生成的地址里去了。
忐忑了一宿，会不会有啥漏洞，币全没了呢？
安慰自己说，如果因为自己生成的地址有问题，导致币被盗，就当学艺不精，交学费了吧。

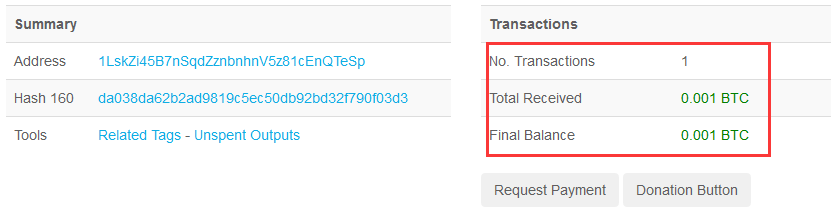
早晨起来一看，还好，币还安在。
那就耐心的等分叉吧

总结

虽然很是折腾，但是这个过程收获不菲，弄懂了好多之前不了解的东西。
这个系列的文章暂时到此为止，写出来容易，学的过程太累。

@deanliu 刘老师过来看看，要不要把你的币都转到我这里来，我帮你免费保管。

This page is synchronized from the post: 谢天谢地，比特币还在，静待分叉

在之前的帖子中： 每天进步一点点： 比特币的公钥压缩与地址
在文末抛出一个问题，也是我迫切想知道的疑问

就是一个原始的私钥，可以生成两个公钥（未压缩的和压缩的)
而这两个公钥可以分别用来生成比特币地址

• 对应未压缩公钥的地址
• 对应压缩公钥的地址

我的疑问就是：

两个地址对应的是同一个私钥(256bit随机数)，那么我向一个地址打一笔钱过去，是两个地址同时显示有钱，还是只是我打钱的地址有钱呢？

等了半天也没见有人回答我这个问题。
不如动手试试吧

操作步骤

步骤一：

生成两组私钥以及两个对应的地址：

(咦，为何没贴私钥呢?)

步骤二：

将两个地址对应私钥导入blockchain.info 钱包
并将两个地址分别命名Address(C)， Address(U)

步骤三：

从钱包中转0.001 BTC 给地址： Address(C)

步骤四：

确认转账

步骤五：

查看Address(C)，里边有交易，有余额

步骤六：

查看Address(U)，里边无交易，无余额

步骤七：

在钱包中检查

结论

转向地址的BTC，只出现转账时选择的地址，尽管两个地址是同一组原始私钥。
但是这个可能和钱包的实现有关(我瞎猜的)

不管咋说，私钥再手，天下我有！

再测试一下转回去
聪明的小伙伴们，算算我为了这个测试投入多少真金白银啊?
不写了，我趴床上哭一会去。
😭😭😭😭😭😭😭😭😭
😭😭😭😭😭😭😭😭😭
😭😭😭😭😭😭😭😭😭
😭😭😭😭😭😭😭😭😭
😭😭😭😭😭😭😭😭😭

This page is synchronized from the post: 真金白银出真知： 测试一下生成的比特币地址😭😭

在昨天的帖子中，学习了如何由私钥生成公钥.

• 每天进步一点点： 学习比特币的公钥

有朋友私下问我，你咋整出俩公钥啊，一个压缩，一个未压缩，这又是什么鬼？我该用哪个公钥啊？别急，听我慢慢道来。

公钥压缩

为何要压缩

根据我们上节学习的成果，公钥(K)是通过私钥(k)乘以生成点(G)得到的，并且是椭圆曲线上的一个点P(x, y)

上图是我们用Hello World生成的私钥并计算出来的点P
表示成公钥其实就是把加上前缀04并把x和y连接起来

很长很长有木有，一共是520bits (8 + 256 + 256)，使用16进制字符串表示，要130个字节!!
而这么长的内容在网上传输来传输去，传输无数次是很浪费资源的，于是就有了压缩的公钥

为何能压缩

通过以前的学习和上边的分析，我们知道公钥是椭圆曲线上的一个点P(x, y)
而按照椭圆曲线的方程，我们是可以通过x求得y的，所以我们只要保留x部分就可以了
机制就是这么简单！可见数学有多么重要，可惜是我从小学起就没有好好学 😭
同学们千万不要学我!

如何去压缩

以下图示很好的说明了公钥压缩的流程

公钥压缩的示意图( Source: 《Mastering Bitcoin》)

比特币地址

好了，公钥压缩问题已经理解了。
我们继续来进行最后一步，生成比特币地址!!!!

私钥、公钥都有了， 但是要玩转，让别人给我打钱，必须要有地址啊
木有地址，怎么骗钱???, 怎么收钱?

公钥到比特币地址的示意图( Source: 《Mastering Bitcoin》)

《Mastering Bitcoin》好书啊，再次强烈推荐！！

有了这个公钥到比特币地址的流程，生成比特币地址就相当容易了。

从steem python库中扒来ripemd160函数，hashlib真强大啊

1
2
3
4

def ripemd160(s):
        ripemd160 = hashlib.new('ripemd160')
        ripemd160.update(unhexlify(s))
        return ripemd160.digest()

连扒再改弄个了生成地址的函数，请忽略变量命名之类的毛病

1
2
3
4
5

def get_address(public_key):
        pkbin = unhexlify(public_key)
        addressbin = ripemd160(hexlify(hashlib.sha256(pkbin).digest()))
        address = base58CheckEncode(0x00, hexlify(addressbin).decode('ascii'))
        return address

运行我们代码，导入之前生成的两组公钥，得到两个地址：

1
2

Address(C): 1LGWpj3pqbzYWvTLEcBKP6CS5PQkxBgjXj
Address(U): 14EvJWPvFNLnzBBzhm1AG9a5b6XiSBFs6R

验证

导入WIF(未压缩)

在blockchain.info 在线钱包，导入WIF(未压缩)
5K5CpQZtUvPqwk2UE1FAiWC1nPV1WYqMnEhMYy2WTiMz3J1u9nm

再导出私钥，显示的地址是未压缩的，但是私钥自动给显示成WIF-Compressed了
Address(U): 14EvJWPvFNLnzBBzhm1AG9a5b6XiSBFs6R

导入WIF-Compressed

在blockchain.info 在线钱包，导入WIF-Compressed
L2mZAF2AEEfq2cuVAQ5XtBqcTLEdFRWSifT7i6Hf2uZckefDJfp5

再导出私钥，显示的地址是压缩的，私钥显示和我们导入的相同
Address(C): 1LGWpj3pqbzYWvTLEcBKP6CS5PQkxBgjXj

不同的私钥(压缩、未压缩) 对应不同的地址

由此可见，不同的私钥(压缩或者未压缩)对应不同的比特币地址，和我们程序中生成的地址结果一样

钱包里虽然把私钥都作为WIF-Compressed显示，但是对于压缩和未压缩的，是区别对待的。

关于压缩私钥，压缩地址，以及压缩公钥

无论是压缩私钥还是压缩地址，地址和私钥本身是不压缩的，只是代表对应的公钥是压缩的而已

总结

• 公钥压缩可以节省空间
• 公钥压缩的原理: 对应椭圆曲线上的点P(x, y) ， 可以通过x求得点y
• 公钥压缩的实现，y是偶数用02做前缀，奇数03，接上x的16进制字符串表示
• 比特币地址由公钥按固定流程生成
• 压缩公钥生成对应压缩公钥的地址
• 未压缩公钥生成对应未压缩公钥的地址
• blockchain.info 导入相同私钥的WIF， WIF-Compressed，生成两个地址
• 地址和私钥本身是不压缩的，只是代表对应的公钥是压缩的而已

疑问，两个地址对应的是一个私钥(256bit随机数)，那么我向一个地址打一笔钱过去，是两个地址同时显示有钱，还是只是我打钱的地址有钱呢？
我一会用我生成的这俩地址打一个比特币过去测试一下，你们别乱动啊。😭

今天就探索到这里。
免责声明，本文为个人理解，示例仅供参考
因使用文中代码或地址造成的损失，概不负责！

This page is synchronized from the post: 每天进步一点点： 比特币的公钥压缩与地址

中文区网友发了一篇文章，介绍Python piston库

并在其中提出了几个问题。

问题之一：

在查看粉丝的时候，如果某人关注了你，又取消了关注，为什么他／她还会出现在粉丝列表里？

问题之二：

程序获取的Voting Power 很低，为何给别人投票后反而会涨，然后投票会降？

昨天我在他帖子中回复的第二个问题，第一个问题因为需要测试，没有直接回答

get_followers 问题没法重现

很抱歉，才抽出时间测试
经过我的测试，没法重现你帖子中描述的问题

测试之前我有1405个关注者

获取关注者数量，让某人取消关注后再次获取，让某人重新关注后再次获取
从数量上看没有错，我把名单显示出来也没有错

我看了一下steem python 库 以及 piston 库，两者的实现是一样的
都是封装并调用以下两个API

• get_followers
• get_following

steem中两个API定义如下：

1
2

vector< follow_api_obj > get_followers( string to, string start, follow_type type, uint16_t limit )const;
vector< follow_api_obj > get_following( string from, string start, follow_type type, uint16_t limit )const;

我这没法重现你说的问题，建议你重新测试一下
如果还存在，建议提供你的详细代码以及重现步骤

其它

关于Voting Power 问题我已经解答了，就不再赘述了。

Python 库推荐大家用官网的
官网的库是复制piston并经过重构的，更易读
并且HF18后很多新功能，piston里是不支持的

• piston_lib上次更新时间： Latest commit cb94d72 on May 15
• 官网Python库上次更新时间： Latest commit 93ac4db on Jun 24

该如何选择，大家已经有了决定了吧？

This page is synchronized from the post: 回答 @yuxi 关于get_followers 的问题

在之前的文章中，学习了这些东西：

• 学习了一下Base58编解码
• 继续学习Base58以及Base58Check
• 继续学习比特币的私钥 & 私钥的表示方法

尤其是通过最后一篇文章的学习，已经可以生成比特币的私钥，并可以将生成的私钥导入到 blockchain.info 在线钱包，并由此得到比特币地址。通过从blockchain.info 钱包导出私钥与我们获得的私钥对比，我们得知并基本掌握了私钥的几种表示方法。

• HEX
• Base58
• WIF
• WIF-Compressed

椭圆曲线与公钥

提到私钥我们常常提到公钥，他们是成对出现的。
公钥是从私钥通过椭圆曲线运算计算得来的，这个过程是不可逆的。亦即通过私钥可以算出公钥，反之则不行。

( Source: 《Mastering Bitcoin》)
别问我啥意思，不懂，就是看着挺好看是不？

比特币使用NIST(National Institute of Standards and Technology)确定的secp256k1标准中定义的椭圆曲线以及一组数学常量。

( Source: 《Mastering Bitcoin》)

看了一下椭圆曲线的讲解，一头雾水，看来凭我的智商是学不明白了，交给数学家们去研究好了！
我关心的是，如何从私钥到公钥，研究了半天，原来很简单，就是一个公式：
K=k∗G
其中小k是我们的私钥，G是生成点，K是结果亦即公钥是曲线上的另外一个点。

因为生成点对所有的比特币用户都是相同的，所以同一个私钥k乘以生成点G，总会得到相同的公钥K。所以从k到K是确定的，并且只能单向运算。这就是为何比特币地址(由公钥生成)可以告诉任何人不用担心泄露私钥。

Steem 官方Python 库中的实现

1
2
3
4
5
6
7

secret = unhexlify(repr(self._wif))
order = ecdsa.SigningKey.from_string(secret, curve=ecdsa.SECP256k1).curve.generator.order()
p = ecdsa.SigningKey.from_string(secret, curve=ecdsa.SECP256k1).verifying_key.pubkey.point
x_str = ecdsa.util.number_to_string(p.x(), order)
y_str = ecdsa.util.number_to_string(p.y(), order)
compressed = hexlify(bytes(chr(2 + (p.y() & 1)), 'ascii') + x_str).decode('ascii')
uncompressed = hexlify(bytes(chr(4), 'ascii') + x_str + y_str).decode('ascii')

其中repr(self._wif)得到的是HEX形式表示的私钥

导入我们之前生成的私钥试试看：
a591a6d40bf420404a011733cfb7b190d62c65bf0bcda32b57b277d9ad9f146e

我们也会生成公钥了!!!

神马椭圆曲线，神马方程之类的，统统丢一边去吧
作为常年CTRL+C, CTRL+V变成的猿类，不需要了解太高深的数学姿势！
(PS: 数学家们是最值得尊重的了，没有他们的辛苦耕耘，我们就没有这么多好用的数学工具)

《Mastering Bitcoin》中有一个例子，验证点P在secp256k1定义的椭圆曲线上。

我们也来验证一下我们的生成的点P符不符合要求。

完美

示例代码

本文中所使用的代码如下：
感兴趣的朋友可以使用自己的私钥试试来生成公钥玩。

1
2
3
4
5
6
7
8
9
10
11
12
13

import ecdsa
from binascii import hexlify, unhexlify
secret = unhexlify('a591a6d40bf420404a011733cfb7b190d62c65bf0bcda32b57b277d9ad9f146e')
order = ecdsa.SigningKey.from_string(secret, curve=ecdsa.SECP256k1).curve.generator.order()
p = ecdsa.SigningKey.from_string(secret, curve=ecdsa.SECP256k1).verifying_key.pubkey.point
x_str = ecdsa.util.number_to_string(p.x(), order)
y_str = ecdsa.util.number_to_string(p.y(), order)
compressed = hexlify(bytes(chr(2 + (p.y() & 1)), 'ascii') + x_str).decode('ascii')
uncompressed = hexlify(bytes(chr(4), 'ascii') + x_str + y_str).decode('ascii')
p = 115792089237316195423570985008687907853269984665640564039457584007908834671663
x = int(hexlify(x_str).decode('ascii'), 16)
y = int(hexlify(y_str).decode('ascii'), 16)
(x ** 3 + 7 - y**2) % p

总结

• 公钥(K)可以通过椭圆曲线运算由私钥(k)计算得出
• 私钥(k)到公钥(K)计算公式： K=k∗G
• 生成过程使用secp256k1标准中定义的椭圆曲线以及一组数学常量
• 从私钥(k)到公钥(K)结果是确定的，并且只能单向运算
• 使用Python的ecdsa库，可以轻松实现私钥(k)到公钥(K)的计算

今天就探索到这里。
免责声明，本文为个人理解，示例仅供参考
因使用文中代码造成的损失，概不负责！

This page is synchronized from the post: 每天进步一点点： 学习比特币的公钥

之前学习了 Base58编解码 以及Base58Check

总结一下之前的学习成果，那就是

• Bash58编码把大整数，转换成按58进制表示的字符串
  去掉了0 , O , I， l 以及 +, / 易混淆字符
• Base58Check在Base58基础上加上了版本信息以及校验

其实学习这些都是为了学习了了解STEEM以及比特币的地址啥的
今天我们来学习比特币的私钥

私钥即保存金钱的地方

之前我一直没搞懂私钥是啥玩意，听着很高大上有木有
经过一番深入的学习和研究，我终于得出一个惊天地泣鬼神的结论
那就是： 私钥就是保存金钱的地方

注意，不是钱包，是私钥。

为啥这么说呢？
因为即便的钱包保管的很好，只要你的比特币私钥泄露出去，那么你的钱，将不会属于你了。
钱包还在，钱没了，最悲惨的莫过于此吧？

通过进一步的学习，我又有重大发现了
私钥相当于你藏钱的地方，而地址是你收钱的入口
任何人都可以往地址这个入口里扔钱，但是没法往出掏钱
只有拥有私钥的人才可以。

再进一步学习，发现地址是由私钥产生的，而通过地址却无法计算得出私钥
就是说私钥到地址的过程是单向不可逆的。

私钥就是一个256位数字

说了半天，私钥到底是啥，其实私钥就是一个256位，取值处于1到n - 1之间的随机数
其中： n = 1.158 10⁷⁷*

搞了半天就是一个256位数字嘛。
据说sha256，就能轻易生成个256位随机数，那么是不是就可以用来产生私钥呢？
看了一下《Mastering Bitcoin》，果然可以
大致意思就是把随机源收集的比特串送给sha256来生成256位数，并判断是否处于1到n - 1之间。

让我用Hello World做比特串来生成一个试试

1
2
3
4
5

>>> import hashlib
>>> from binascii import hexlify, unhexlify
>>> s = hashlib.sha256(bytes('Hello World', 'utf-8')).digest()
>>> print(hexlify(s).decode('ascii'))
a591a6d40bf420404a011733cfb7b190d62c65bf0bcda32b57b277d9ad9f146e

哈哈哈哈哈，我们也有私钥啦。

这个是真的私钥哦，可以导入钱包的哦

导入试试看，耶，咱也有比特币地址啦

去blockchain.info看了一下，居然，竟然真的有四笔交易
向伟大的程序员致敬！向Hello World致敬！
https://blockchain.info/address/1LGWpj3pqbzYWvTLEcBKP6CS5PQkxBgjXj

私钥的表示方法

然后我们在回头来看blockchain.info里的钱包

我哭了，无论选择哪种方式，都不是我导入的私钥呀，我的私钥哪里去了?
于是又仔细学习了一下，原来除了直接用字符串形式的数字

私钥还可以有不同的表示方式！
比如说上边两个图列出的

• WIF
• Base58

咦，知道我为啥学习Base58了吧！

Base58

先来看看Base58，Base58就是把生成的私钥串使用Base58编码

引入我们上一篇文章学的Base58编码
对a591a6d40bf420404a011733cfb7b190d62c65bf0bcda32b57b277d9ad9f146e进行编码
结果如下：

和上边Base58编码完全一样有木有？

WIF

再来看WIF
WIF亦即： Wallet Import Format (WIF)

再次强烈推荐《Mastering Bitcoin》，我想要的它都讲

其中HEX
应该就是a591a6d40bf420404a011733cfb7b190d62c65bf0bcda32b57b277d9ad9f146e

WIF看图就是加上前缀加上校验码嘛，然后用Base58Check编码

知道为啥学Base58Check了吧？

试了一下生成的东西为：

而BlockChain的钱包里的开头是L, 很明显我这个是未经压缩的

咋压缩呢？看图是加了个0x01后缀，然后再编码，让我试试试看

完全一样有木有！
话说, Blockchain.info不厚道，明明是WIF-compressed，你非得显示的个WIF，这不是误导我呢吗？差评！

总结

• 私钥就是一个256位随机数(处于1到n - 1之间)
• 私钥可以用hashlib.sha256来生成
• 私钥可以表示为64位16进制串、Base58、WIF、WIF-compressed
• 64位16进制串就是把私钥直接转换
• Base58编码就是对64位16进制串直接编码
• WIF就是在64位16进制串对应的字节串前加上前缀0x80， 并用Base58Check编码
• WIF-compressed就是在64位16进制串对应的字节串前加上前缀0x80，并加上后缀0x01， 并用Base58Check编码

好了，今天就学习到这里。
免责声明，本文为个人理解，示例仅供参考
请勿使用文章中写到的地址，如果导致bitcoin损失，概不负责！

This page is synchronized from the post: 继续学习比特币的私钥 & 私钥的表示方法