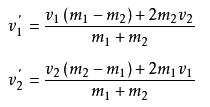在辽大的皇姑校区内，有一条银杏路，每到金秋，银杏叶子变黄落满一地，让银杏路好像铺满黄金一样，所以被大家亲切地称为黄金大道。
每到最适合欣赏满地银杏落叶的季节，辽大都会举办银杏节，来赏银杏拍照的人挤满整条银杏路，并且学校外边的一环也常常因此塞车。
为了错开人流高峰，我三两天前去了辽大，可惜来得有些早，银杏叶还不是那么黄，也没有落下来几片，黄金大道，没有黄金。
除了银杏，辽大院内还有一些枫树之类的观赏树木，红红的一片也挺好看。
不过相比银杏路的知名度，红枫们只能做为陪衬啦。
其实校园里走一走，到处都是风景，看着学子们朝气蓬勃的样子，感觉自己也年轻了十好几岁呢。
年轻真好呀！
oflyhigh and click VOTE
This page is synchronized from the post: ‘黄金大道没有黄金’
看到一个博主讲了一件很有意思的事情，大意是两个方块物体在水平方向上弹性碰撞后，其中一块再撞到墙壁反弹，最终会发现，在一定条件下发生弹性碰撞的次数会和PI这个常量极度相关。
(图源 ：pixabay)
为了说明这个问题，我大致画了个图（原谅我的绘图技能）：
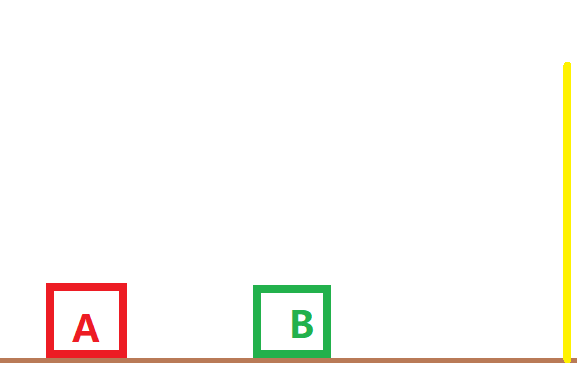
在上图中，有红色方块A(1)和绿色方块B(2)，A以速度v1前进，B静止不动(速度v2=0)，A撞击到B，B被撞后获取一定的速度vb，方块B撞击墙体（黄实线）后返回，又撞击A。
如果A、B质量相等，那么撞击会发生3次，如果A的质量大于B，撞击会发生很多次。
而这个博主总结的规律为：
如果A、B质量相等，撞击3次
如果A的质量是B的100倍，那么撞击31次
如果A的质量是B的10000倍，那么撞击314次
如果A的质量是B的1000000倍，那么撞击3141次
如果A的质量是B的100000000倍，那么撞击31415次
观察撞击次数就会发现，撞击的次数竟然符合圆周率(PI)的规律。
其实如果是真实地实验，很难重现上述规律，为何？因为方块和平面之间存在摩擦，方块在空气中也会有空气阻力，方块和方块撞击时可能会发生一定程度的形变等等。
所以只有在理想情况下，才可能重现上述规律。那么什么是理想情况呢？就是不存在摩擦、不存在空气阻力、方块撞击时无形变等等。
百度百科里关于弹性碰撞定义的更科学一些，直接搬来：
在理想情况下，物体碰撞后，形变能够恢复，不发热、发声，没有动能损失，这种碰撞称为弹性碰撞（elastic collision），又称完全弹性碰撞（Perfect Elastic Collision）。
弹性碰撞符合两大物理定律：动量守恒定律 以及能量守恒定律
而根据我们描述的情况，不难推导出，弹性碰撞后物体的速度：
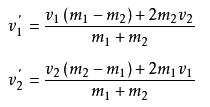
因为我们目的不是推导公式，所以直接拿来用就好了。因为我们例子中碰撞是发生在直线上的核心碰撞，所以公式中的v，就是物体的初速度啦。
说了这么多，我是要证明弹性碰撞和圆周率的关系吗？非也！我只是好奇碰撞真的符合这个规律吗？
之前说了，理想情况下，实验才能重现出响应的规律，但是实际上没法弄出理想的实验条件呀？不过没关系，可以用程序模拟啊！
为了计算碰撞次数，我们首先需要计算碰撞前后的速度（其实就是简单地套用公式）：
1 | def collision(m1, v1, m2, v2): |
接下来是计算碰撞次数，这可难住了我，如何计算碰撞次数呢？其实就是找出符合什么条件会退出碰撞？
从方块图中，我们不难分析出，只有当方块A向左侧行走，且方块B追不上它时，碰撞才会结束，假设向右运动为正，那么亦即符合如下条件：
v1 < 0 and v2<=0 and abs(v1) >= abs(v2)
还有就是方块和墙壁撞击，墙壁的质量，那么代入速度公式中，不难算出：
`v2 = -1v2`*
根据上述分析我写出如下代码来计算次数：
1 | def func_times(m1, v1, m2, v2): |
好了，现在是见证奇迹的时刻的时刻啦。
1 | m1 = 100 |
给木块设定质量和初速度，然后模拟碰撞，看看是不是符合这个博主说的规律？
运行上述程序，输出如下：
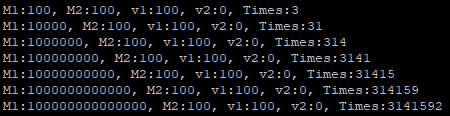
哇哇哇，果然是圆周率啊，是不是很神奇？
(图源 ：pixabay)
至于为何是圆周率，就留给聪明的你去证明啦！
oflyhigh and click VOTEThis page is synchronized from the post: ‘有多无聊：弹性碰撞与Python代码’
前段时间，一位朋友家的老款液晶电视坏掉了，然后拿到我那个开车会馆的朋友那里，打算让他帮忙修理一下。
朋友大包大揽的应承下来，然后把电视拆开，弄坏了一个精密的小部件，并晾了好多天之后，无奈送到修理铺去了。
为此我嘲笑了他好多天，明明是修车的，竟然搞起了修理家电，真要修好了也行，反而让电视坏得更严重了，哈哈。
不过话说我家也有个坏掉的液晶电视，就是突然间电源灯就不亮了，因为家里好几个电视，所以就这么坏着也没搭理它，已经闲置一两年了。
不过因为朋友给朋友修电视这个事，我突然想起了我这个电视，我觉得我这个电视应该不是什么大故障，有可能就是电源板上的保险丝之类坏掉了，按说修起来应该不复杂吧？
于是乎废了九牛二虎之力把液晶电视后盖拆开，找到了电源板，并且找到了保险丝的位置。然后从自己的一堆保险丝中选择了一个3A的保险丝替换上去。胆颤心惊地插上电源并且按起Power 键，结果竟然还是一点响应都没有。
于是乎想着找万用表测试一下电源板的输出之类的，可是找了半天也没找到我的万用表哪里去了。后来想到其实这个破电视我2年没开机我也没觉得有啥问题，收拾它有啥意义呢？
于是乎，果断放弃，将机器重新安装回去。收获了腰酸背痛之外，还明白了不要去做没什么意义的事情，还有就是自己终究不是万能的。
不过我觉得这件事对我朋友们保密，否则一定会被他们嘲笑死的，毕竟我之前嘲笑他那么久呢，哈哈哈哈哈。
oflyhigh and click VOTEThis page is synchronized from the post: ‘终究不是万能的’
京东商城有个栏目叫做京东秒杀，每两小时推出一场秒杀活动。最近几年，临睡前看看京东秒杀，淘点自己喜欢的东西已经成为了习惯。
(图源 ：pexels.com)
可是这两年，越来越觉得京东秒杀栏目下每什么新东西，基本全是一些笔记本电脑啊、电脑硬件啊、手机啊、汽车用品啊等等。
有时候恰恰自己访问过的关注过的商品出现在秒杀栏目，我还不胜欣喜，赶紧抢购下来。不过当发现自己偶尔访问的商品频繁出现在秒杀栏目下，我越发觉得不对劲了。
有一天实在忍不住，那媳妇的手机，看一下她的京东APP下的京东秒杀，发现她的京东秒杀下全是一些衣服、化妆品、小学生教辅资料，我才明白，我们都被大数据给套路了。
无独有偶，对比一下我们的网易新闻APP，发现我这网易新闻里推的大多是一些比特币、虚拟币等相关信息，而她的网易新闻里推的更多是一些明星的小道消息。
至于淘宝APP就更不用说，我进到我的淘宝APP首页，会觉得整个淘宝都是卖电脑和电子模块的，什么树莓派啊、香蕉派啊、Arduino啊等等。
以前看过一篇分析文章，大意是说抖音、快手之类的会通过分析用户行为，迎合用户喜好，不断调整推送给用户的内容，让用户始终处于一个舒适区，爽得停不下来。
那么不用分析，从我自身的经历来看，京东、网易、淘宝，也都使用相应的策略，推送给用户系统认为用户喜欢的内容。
但是这样的策略真的有效嘛？我承认一开始属实吸引了我，看到自己想看的新闻，看到自己关注的商品出现在秒杀中……
但是久而久之，每天都看相似的商品，每天都看雷同的新闻，时间长了想不厌烦都难啊，就想是一句歌词里唱的那样：
就算是山珍海味老吃也会烦
所以这些商家自做聪明的使用大数据，使用用户行为分析来迎合用户的行为，长远来看，倒可能是把用户驱离的一种失败策略。
(图源 ：pexels.com)
不过，估计以后商家们也会意识到这点吧，有可能会对策略进行升级和调整。哎，不管咋说，我还是讨厌这个东西！
oflyhigh and click VOTEThis page is synchronized from the post: ‘可恶的大数据与用户行为分析’
好久之前去丁香湖，曾经拍下我认为超级有意境的一张照片，前两天去丁香湖，我又特意去上次拍照片的地方，同一位置同一角度，拍了同样一张照片。
不过如果说之前拍出来的犹如童话，那么这次拍出来的照片一下子被打回到现实。
找一下之前的照片对比一下：
看了一下，天空基本上还是那么蓝，水面也还是那么开阔，火车道什么的也没有什么变化。
唯一有变化的就是原本岸边的绿草要么变成了光秃秃的土地，要么变得枯黄，就是这一点，让原本美好的风景大打折扣。
哎，可见绿化有多么重要啊，顺便再贴几张照片吧。
虽然因为少了许多绿色，看起来没那么美，不过胜在天高云淡，还是让人觉得挺舒服的。
oflyhigh and click VOTEThis page is synchronized from the post: ‘绿化有多重要’
昨天在微信群里浅水，看他们聊天，突然说到了IPv6地址，一个朋友说到IPv6取之不尽用之不竭，另一个朋友说了一句话：IPv6可以给每个原子编个号。
(图源 ：pixabay)
好吧，因为宇宙是非常大的，甚至凭我的大脑都很难想象宇宙有多大，诺大的宇宙当中有多少星球有多少原子更不必说了，所以我认为朋友的意思应该是IPv6可以给地球上的每个原子编个号。
那么IPv6真的可以给地球上的每个原子编个号嘛？我觉得有点夸张，于是就想验证一下。
首先，有多少个IPv6地址呢？
我们知道IPv6的地址长度有128位，所以理论上会有2128，这么多个地址。
如果用Python语言来计算的话，那么IPv6为：
ipv6=2**128
等于这么多个（请原谅我根本数不过来）😳：
340282366920938463463374607431768211456
知道了IPv6地址的数量，我们再来估算一下地球上有多少个原子。要想知道这个，我想到的办法是计算一下地球的体积，再除以原子的体积。
那么地球的体积是多少呢？由于太阳引力的问题，地球不是个正规的圆球，百度百科相关描述如下：
地球赤道半径6378.137千米，极半径6356.752千米，平均半径约6371千米。
反正是估算，那么我们就按它是个规则的圆球好了，使用平均半径6371千米作为圆球半径。
圆球体积的计算公式我们小学都学习过：
用Python计算，地球体积：
from math import pi as PIr = 6371 * 1000earth_v = 4/3*PI*(r**3)
也就是说，地球体积大致为这么多立方米(M2)：
1.0832069168457536e+21
注：大气层中也有原子，上述体积没有计算大气层，不过反正是估算嘛。
地球体积足够大了，但是原子的体积可是足够小的啊。学习初中化学的时候，我们就知道了，不同原子的大小是不一样的啦。
从百度上找了半天资料，普遍的说法是一般来讲，原子的半径约为10-10m，当然了，这个值肯定不是精确的，但是反正我们是估算，数量级差不多就行啦。
用Python计算，原子体积：
r_atom = 10**(-10)atom_v = 4/3*PI*(r_atom**3)
计算出来原子的体积约为这么多立方米(M2)：
4.188790204786391e-30
所以，地球上的原子个数估算为：
atom_c = earth_v / atom_v
也就是说初略估算，地球上原子数量约为（个）：
2.5859660281099996e+50
这时候我们再来看看IPv6是否可以分配到地球上的每一个原子：
ratio = ipv6 / atom_c
计算出来的结果为：
1.3158810410577592e-12
也就是说，IPv6 地址远远不够分配到地球上的每一个原子上。
IPv6 地址远远不够分配到地球上的每一个原子上。
不过关于IPv6地址还有一个说法：
IPv6地址数量号称可以为全世界的每一粒沙子编上一个地址。
(引用来源：
(图源 ：pixabay)
假设地球都是由沙子组成，假设沙子的半径是均匀的0.01mm，那么大致估算下来，那么每粒沙子大致可以分配到1315个地址，看来，真的可以给每一粒沙子编上一个地址。
（本文仅供无聊消遣，不保证方法和计算一定无误，欢迎专家批评指正）
oflyhigh and click VOTEThis page is synchronized from the post: ‘有多无聊：IPv6地址和原子’
Update your browser to view this website correctly. Update my browser now